通观本书,我们已经遇见过许多不同的问题,而且在面对每一个问题时,都采用了一种最适合于解决该问题的算法。在某些例子中,我们还须要对参数进行调整,或者借助于优化手段来找出一个满意的参数集来。本章将考查一种截然不同的问题解决方法。与先前遇到一个问题就选择一种算法的思路不同,我们将编写一个程序,尝试自动构造出解决某一问题的最佳程序来。因而从本质上看,我们即将要构造的是一个能够构造算法的算法。
遗传编程 #
遗传编程或称基因编程,简称GP,是一种从生物演化过程得到灵感的自动化生成和选择计算机程序来完成用户定义的任务的技术。从理论上讲,人类用遗传编程只需要告诉计算机“需要完成什么”,而不用告诉它“如何去完成”,最终可能实现真正意义上的人工智能:自动化的发明机器。
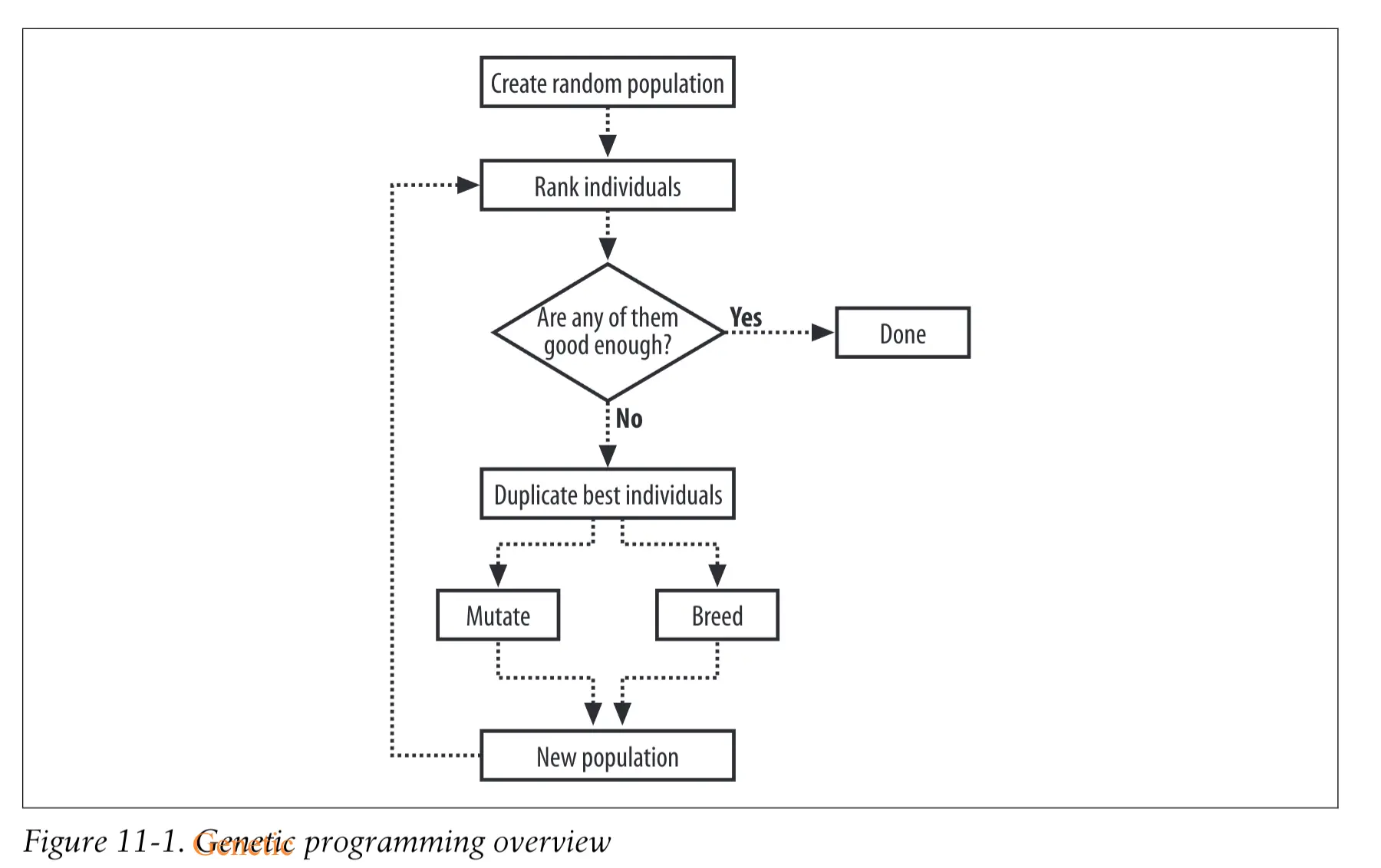
程序以树的形式表示 #
为了构造出能够用以测试、变异和配对的程序,我们需要一种方法能够在Pyho如代码中描述和运行这些程序。这种描述方法自身必须是易于修改的,而且更重要的一点是,它必须保证所描述的是一个实实在在的程序一这意味着,试图将随机生成的字符串作为Python代码的做法是行不通的。为了描述遗传编程中的程序,研究者已经提出了各种不同的方法,而这其中应用最为普遍的是树形表示法。
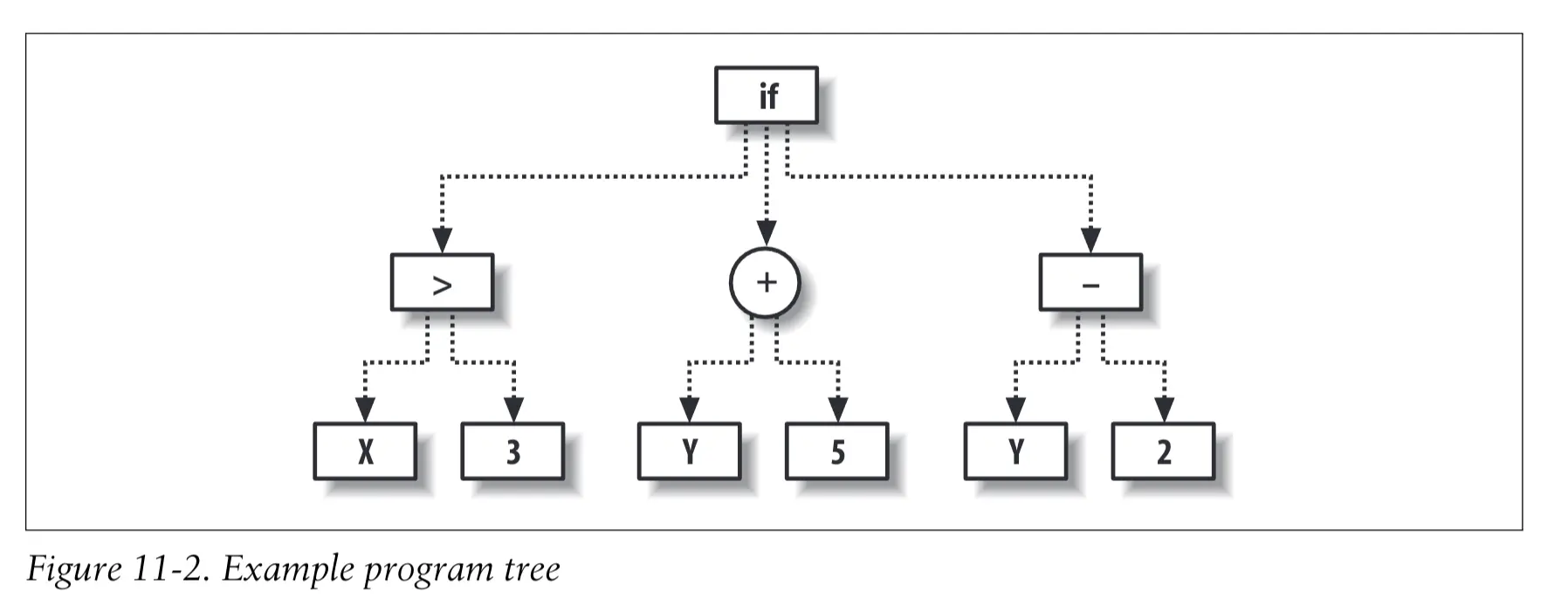
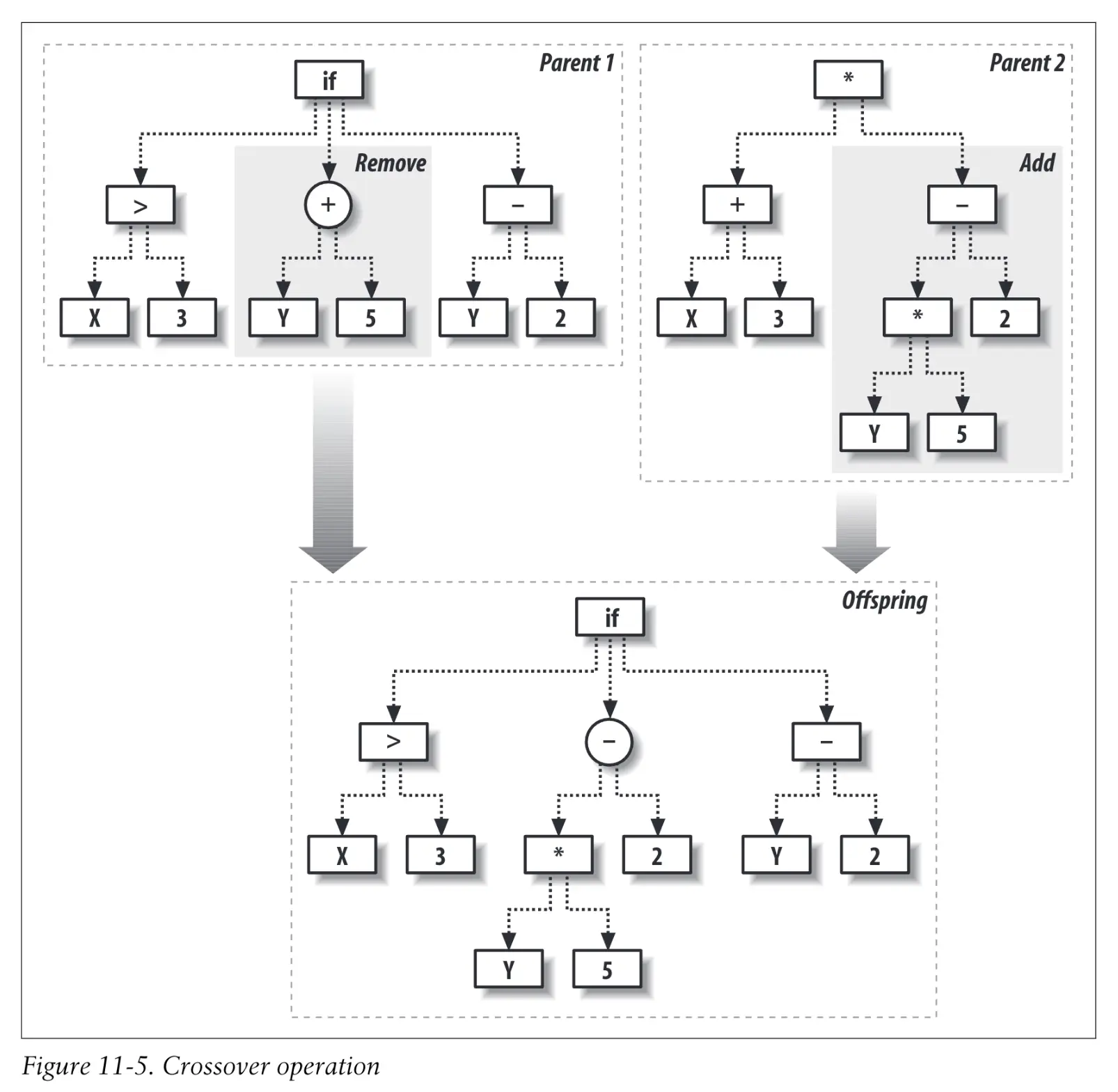
这个图上的代码就等价于
def func(x,y)
if x > 3:
return y + 5
else:
return y - 2
定义的结构如下 gp.py
from random import random,randint,choice
from copy import deepcopy
from math import log
# 封装类,用于描述一个函数
class fwrapper:
def __init__(self,function,childcount,name):
self.function=function
self.childcount=childcount
self.name=name
# 节点
class node:
def __init__(self,fw,children):
self.function=fw.function
self.name=fw.name
self.children=children
def evaluate(self,inp):
results=[n.evaluate(inp) for n in self.children]
return self.function(results)
# 参数节点
class paramnode:
def __init__(self,idx):
self.idx=idx
def evaluate(self,inp):
return inp[self.idx]
def display(self,indent=0):
print '%sp%d' % (' '*indent,self.idx)
# 常量节点
class constnode:
def __init__(self,v):
self.v=v
def evaluate(self,inp):
return self.v
def display(self,indent=0):
print '%s%d' % (' '*indent,self.v)
然后再定一些节点操作
addw=fwrapper(lambda l:l[0]+l[1],2,'add')
subw=fwrapper(lambda l:l[0]-l[1],2,'subtract')
mulw=fwrapper(lambda l:l[0]*l[1],2,'multiply')
def iffunc(l):
if l[0]>0: return l[1]
else: return l[2]
ifw=fwrapper(iffunc,3,'if')
def isgreater(l):
if l[0]>l[1]: return 1
else: return 0
gtw=fwrapper(isgreater,2,'isgreater')
flist=[addw,mulw,ifw,gtw,subw]
那我们就可以用这个来构造一个树了,比如例子
def exampletree():
return node(ifw,[
node(gtw,[paramnode(0),constnode(3)]),
node(addw,[paramnode(1),constnode(5)]),
node(subw,[paramnode(1),constnode(2)]),
]
)
程序的展示 #
def display(self,indent=0):
print (' '*indent)+self.name
for c in self.children:
c.display(indent+1)
构建初始种群 #
我们使用随机的方式构造初始种群,这一过程以递归的方式进行定义
flist=[addw,mulw,ifw,gtw,subw]
def makerandomtree(pc,maxdepth=4,fpr=0.5,ppr=0.6):
if random()<fpr and maxdepth>0:
# 从可用的选择里面随机选一个
f=choice(flist)
构建子节点
children=[makerandomtree(pc,maxdepth-1,fpr,ppr)
for i in range(f.childcount)]
return node(f,children)
elif random()<ppr:
return paramnode(randint(0,pc-1))
else:
return constnode(randint(0,10))
测试解题 #
简单的数学测试 #

首先我们需要一个可以定程序好坏的方式(成本函数)
def scorefunction(tree,s):
dif=0
for data in s:
v=tree.evaluate([data[0],data[1]])
dif+=abs(v-data[2])
return dif
变异 #
当表现最好的程序被选定之后,它们就会被复制并修改以进入到下一代。如前所述,变异的做法是对某个程序进行少许的修改。一个树状程序可以有多种修改方式一我们可以改变节点上的函数,也可以改变节点的分支。
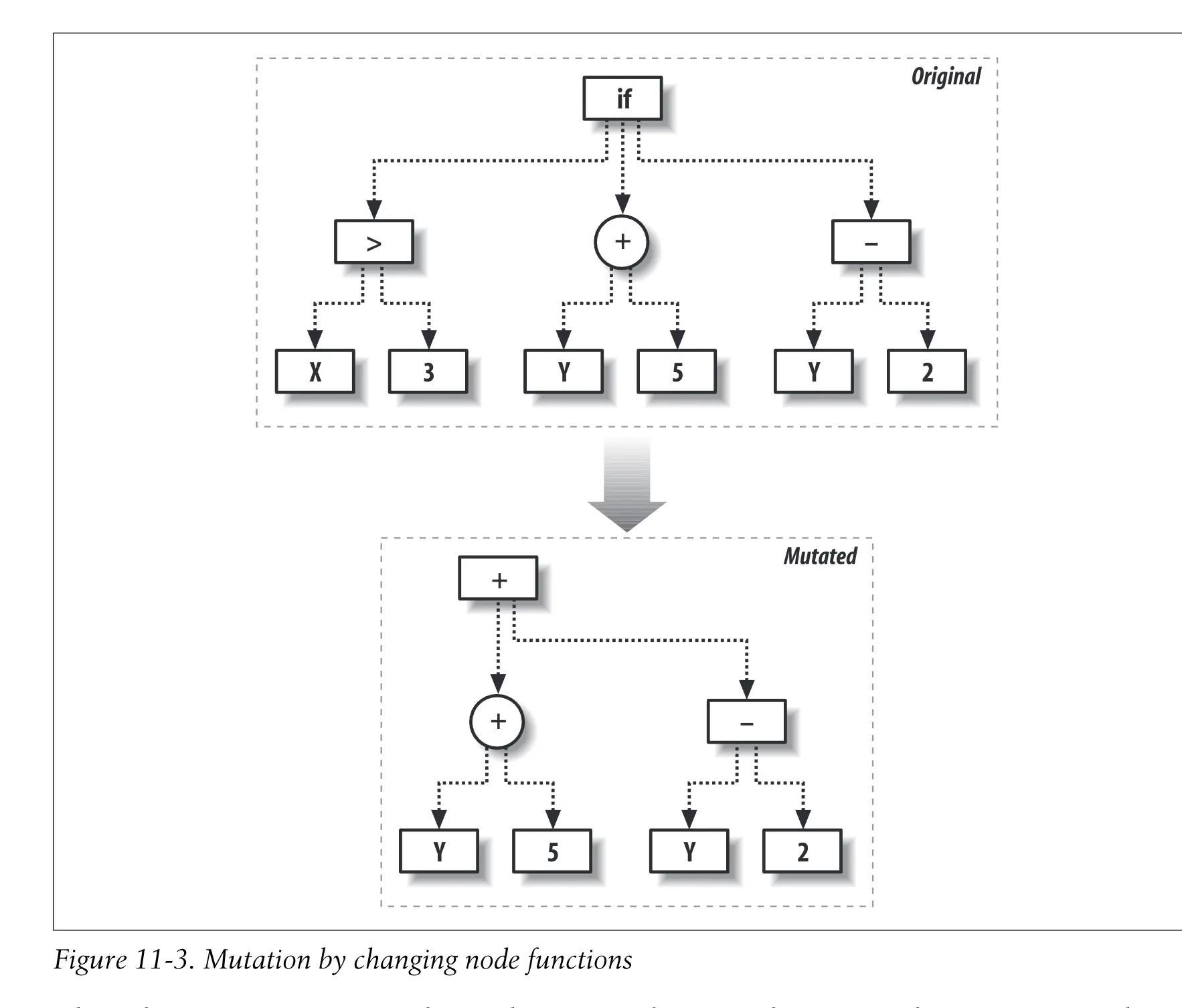
# t = 数, pc = 参数大小
def mutate(t,pc,probchange=0.1):
# 判断是否需要变异
if random()<probchange:
return makerandomtree(pc)
else:
result=deepcopy(t)
if hasattr(t,"children"):
result.children=[mutate(c,pc,probchange) for c in t.children]
return result
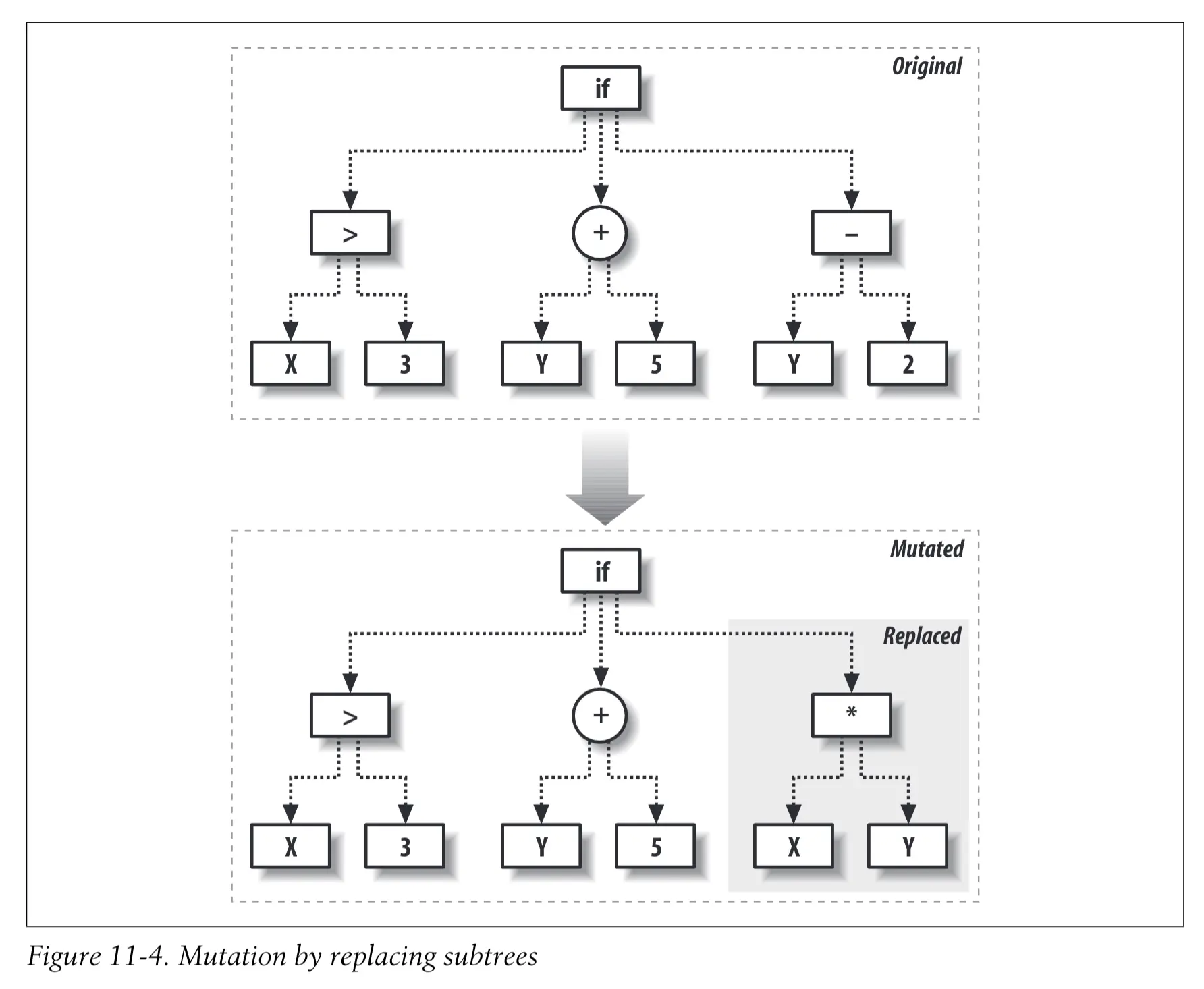
交叉 #
def crossover(t1,t2,probswap=0.7,top=1):
if random()<probswap and not top:
return deepcopy(t2)
else:
result=deepcopy(t1)
if hasattr(t1,'children') and hasattr(t2,'children'):
result.children=[crossover(c,choice(t2.children),probswap,0)
for c in t1.children]
return result
进化算法 #
def evolve(pc,popsize,rankfunction,maxgen=500,
mutationrate=0.1,breedingrate=0.4,pexp=0.7,pnew=0.05):
# 返回一个随机数,pexp越小,随机数越小
def selectindex():
return int(log(random())/log(pexp))
# 随机一个初始种群
population=[makerandomtree(pc) for i in range(popsize)]
for i in range(maxgen):
scores=rankfunction(population)
print scores[0][0]
if scores[0][0]==0: break
# 两个最优解
newpop=[scores[0][1],scores[1][1]]
# 构建下一代
while len(newpop)<popsize:
if random()>pnew:
newpop.append(mutate(
crossover(scores[selectindex()][1],
scores[selectindex()][1],
probswap=breedingrate),
pc,probchange=mutationrate))
else:
# 增加一个随机值,为了多样性
newpop.append(makerandomtree(pc))
population=newpop
scores[0][1].display()
return scores[0][1]
简单游戏 #
本文后面还介绍了一个简单的游戏,这里就略过了,可以参考 gp.py