发现独立特性

迄今为止，除了第3章介绍的聚类算法属于非监督技术外，其余大部分章节都主要集中在监督分类器的讨论上。本章将研究如何在数据集并未明确标识结果的前提下，从中提取出重要的潜在特征来。和聚类一样，这些方法的目的不是为了预测，而是要尝试对数据进行特征识别，并且告诉我们值得关注的重要信息。

本章节也比较的水 ~

数据源 #

这里找了一些数据的源头进行采集，这里就不做过渡的阐述。

Non-Negative Matrix Factorization 非负矩阵分解 #

目前为止，我们手中所持有的是一个带单词计数信息的文章矩阵。而我们的目标是要对这个矩阵进行因式分解，即：找到两个更小的矩阵，使得二者相乘以得到原来的矩阵。这两个矩阵分别是特征矩阵和权重矩阵。

特征矩阵：在该矩阵中，每个特征对应一行，每个单词对应一列。矩阵中的数字代表了某个单词相对于某个特征的重要程度。由于每个特征都应该对应于在一组文章中出现的某个主题，因此假如有一篇文章报道了一个新的电视秀节目，那么也许我们会期望这篇文章相对于单词“television’”能够有一个较高的权重值。

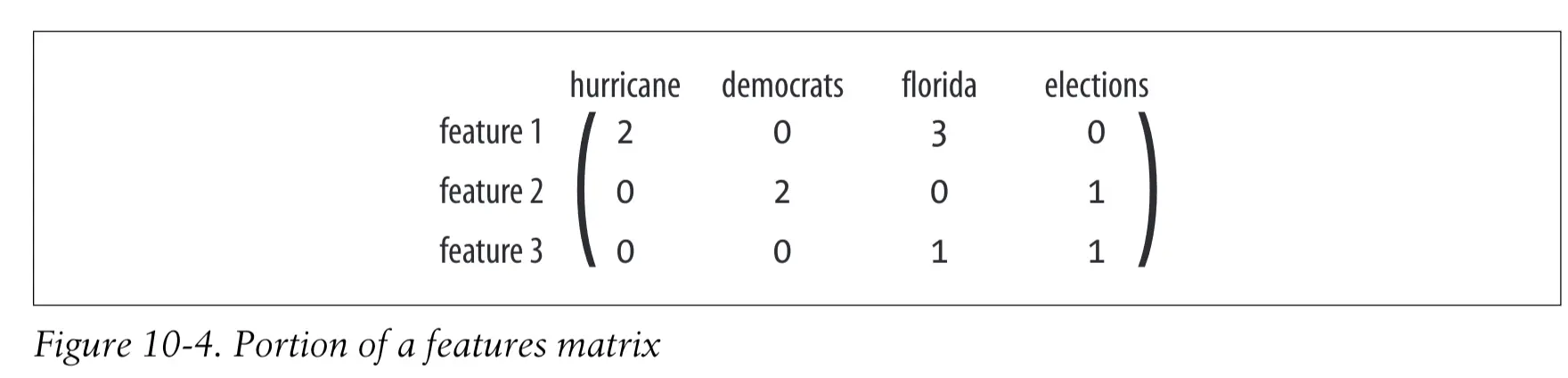
权重矩阵：该矩阵的作用是将特征映射到文章矩阵。其中每一行对应于一篇文章，每一列对应于一个特征。矩阵中的数字代表了，将每个特征应用于每篇文章的程度。

这两个矩阵进行相乘就可以获得如下的结果

算法实现 #

首先定义一个 difcost ，用来计算和理想值之间的差值

def difcost(a,b):
  dif=0
  for i in range(shape(a)[0]):
    for j in range(shape(a)[1]):
      # 差值相加
      dif+=pow(a[i,j]-b[i,j],2)
  return dif

然后我们需要一个成本函数，保证我们的目标是最小化，这里使用了 乘法更新法则

def factorize(v,pc=10,iter=50):
  ic=shape(v)[0]
  fc=shape(v)[1]

  # 随机初始化矩阵
  w=matrix([[random.random() for j in range(pc)] for i in range(ic)])
  h=matrix([[random.random() for i in range(fc)] for i in range(pc)])

  # 设置一个最大迭代次数
  for i in range(iter):
    wh=w*h
    
    # 计算和目标的差值
    cost=difcost(v,wh)
    
    # 每 10 轮打印一次
    if i%10==0: print cost
    
    # 完美解直接返回
    if cost==0: break
    
    # 更新特征矩阵
    hn=(transpose(w)*v)
    hd=(transpose(w)*w*h)
  
    h=matrix(array(h)*array(hn)/array(hd))

    # 更新权重矩阵
    wn=(v*transpose(h))
    wd=(w*h*transpose(h))

    w=matrix(array(w)*array(wn)/array(wd))  
    
  return w,h